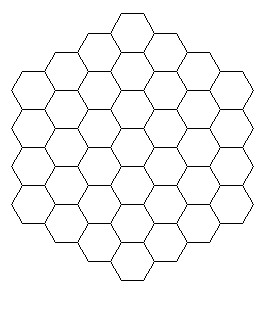
Euler Getter is a mathematical boarod game, which I introduced in 2010, insspired by the game Hex. This game is played by two players on a hexagonal board like:

Thinking of the board as the projective plane, players compete in the Euler characteristics of their regions.
You can play Euler Getter at the following website, containing also variants, some played on surfaces different from the projective plane and some having different cell patterns:
I explain below, the rules, a way to compute the Euler Characteristic and some mathematical background. See also:
Introduction to Euler Getter (Slides of my talk)
One identifies two cells on the periphery in symmetric positions.In the following figure, two cells with the same letter are identified.
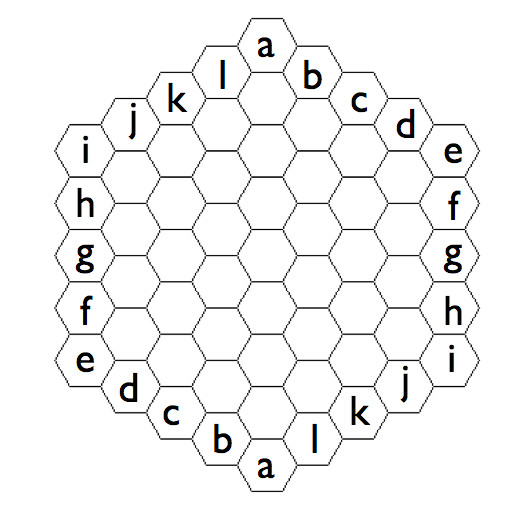
Namely the board expresses a subdivision of the real projective plane into a polygonal complex. (In fact, one can play Euler Getter on any polygonal subdivision of a closed surface of odd Euler characteristic such that each vertex is adjacent to exactly three edges. See Mathematical background below.)
Each player has an allocated color, say red and blue. Players take turns placing a stone(s) of their color on a vacant cell. (If you put a stone on a cell on the periphery, do not forget to put a stone also on the cell in the symmetric position.) The game ends when stones are placed on all cells. Now the projective plane is divided into the red and blue areas. The winner is the one whose area has larger Euler characteristic than opponent's one. (You can play another game where the last rule is reversed.)
The simplest way is to use the polygonal complex structure which the board originally has, and to compute \[ \sharp\{\text{vertices}\}-\sharp\{\text{edges}\}+\sharp\{\text{cells}\}\quad(\sharp\{...\}\text{ means the number of ...}) \] for each of the red and blue areas. This computation seems easy for computers but hard for humans.
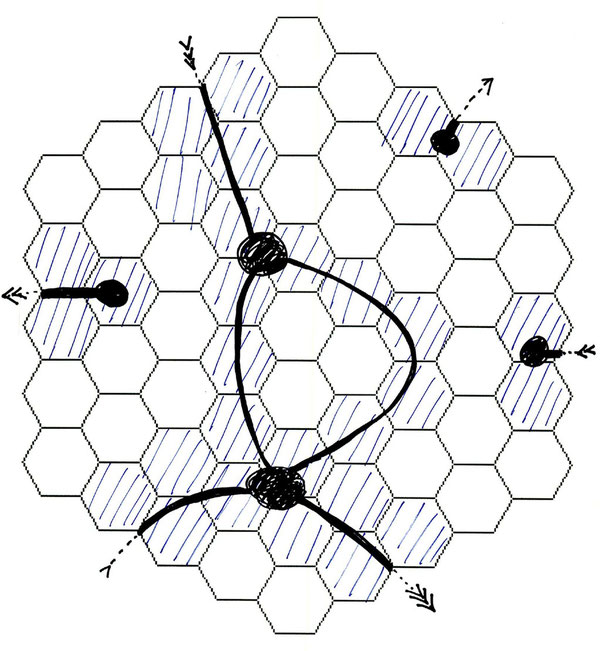
An alternative human-friendly way is to deformation retract an area to a finite graph and compute \[ \sharp\{\text{vertices}\}-\sharp\{\text{edges}\} \] for the graph. For instance, in the following figure, the blue area deformation retracts to a graph with \(5\) vertices and \(5\) edges, and has Euler characteristic zero.
Let \(R\) and \(B\) be the red and blue areas containing their boundaries, so that \(R\cup B\) is the whole projective plane \(\mathbb{P}^{2}\) and \(R\cap B\) is the border of the two areas. From the inclusion-exclusion principle, we have \[ \chi(R)+\chi(B)-\chi(R\cap B)=\chi(\mathbb{P}^{2}). \] Here \(\chi(?)\) denotes the Euler characteristic. The projective plane has Euler characteristic \(1\). On the other hand, because \(\mathbb{P}^{2}\) is a closed surface and each vertex is adjacent to three edges, the border \(R\cap B\) is homeomorphic to the disjoint union of circles and has Euler characteristic \(0\). So \(\chi(R)+\chi(B)=1\), in particular, \(\chi(R)\ne\chi(B)\). This shows that the game never ends in a tie.