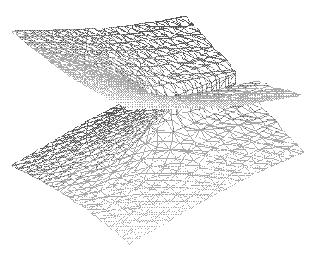
これは複素数体上の空間のもっとも単純な被覆であり、 下方の水平な平面(複素平面)の上に写像されている。 原点における分岐点をはなれると, その平面上の各点の上方に 2個ずつの点をもっている。この空間は、そのような点の対を 置き換えるという操作を許す対称性をもっている。 この絵の空間は、実は複素2次元の空間(それは実4次元をもつ) の中に存在しているが、ここでは実3次元の空間にあるように 投影してみている。 |
|
この研究領域では、数学的な対称性に関わる2つの分野 --- ガロア理論における代数的な対称性、 基本群の理論における幾何学的な対称性 --- をひとつの共通の場に持ち込む。 この2つのいずれの分野においても、数学的対象はそれぞれの対称性 が取る形態を調べることで研究することができるが、 ここでの中心的な主題は、この両分野がお互いに相互作用をおよぼし、 代数は幾何の影響のもとで応用され、また幾何は代数の恩恵のもとで 構築されることではじめて取り扱うことができるような問題 を研究することである。 |

これは複素数体上の空間のもっとも単純な被覆であり、 下方の水平な平面(複素平面)の上に写像されている。 原点における分岐点をはなれると, その平面上の各点の上方に 2個ずつの点をもっている。この空間は、そのような点の対を 置き換えるという操作を許す対称性をもっている。 この絵の空間は、実は複素2次元の空間(それは実4次元をもつ) の中に存在しているが、ここでは実3次元の空間にあるように 投影してみている。 |
|
歴史的には、ガロア理論は代数方程式の研究から生まれた。 古代人は2次方程式を解く公式を知っていたが、ルネッサンス期までには 3次と4次の方程式に対する解の公式も発見された。 19世紀の前半には、エヴァリスト・ガロアにより、 今日ガロア理論として知られる理論が展開される中で、 より高次の方程式に対して(累乗根を用いて解く)公式がない という事実 --- 単にそれまでの技術で知られていないという のではなく、そのような公式が原理的にあり得ないということ --- が明らかにされた。 このような代数的成果は、ある5次方程式が正20面体の対称性と 同じ群をもち、この群が(ある適切な技術的意味で)「可解」でない、 という事実に基づいている。 ガロア理論のアイデアのより親しみやすい例としては、 もうひとつの古典問題の謎解き --- 一般的な角を定規とコンパスだけで3等分できない --- と関係している。 これらの応用はどちらも、代数と幾何の、対称性を通じた相互作用を 物語っている。 |
|
|
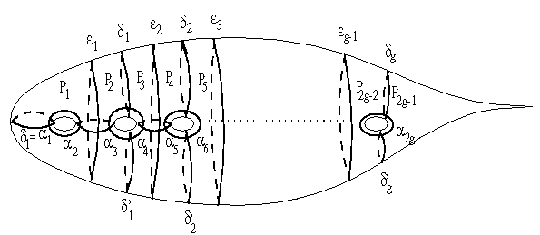
幾何学とくに位相幾何学における基本群の理論は、被覆空間の概念と関係している。 例としては、渦巻き階段の形をしたヘリックス曲線とよばれるものがある。 ヘリックス曲線の各点は、固定されたひとつの円の下方から上方にかけて 渦巻きのように配置してあり、 ヘリックス曲線全体は各点を一周り上の点にもっていく操作に対応する対称性をもつ。 このとき、すべての対称性のなす群は整数の全体と対応し、例えば整数5は 5回転分だけ上に移動することに対応している。 こうした状況を、ヘリックス曲線は円の被覆空間であり、整数全体(のなす 加法群)は円の「基本群」であるという。 空間は、その基本群によって研究することができる。--- 例えば、 もし2つの空間が異なる基本群を持つことが示されれば、 それらの空間は違うということがわかる。 さらに、空間の間の写像(例えばヘリックスから円への写像)も 付随する対称性の群を用いて研究することができる。 |
被覆空間たちは、かなり複雑であり、区別するのも容易でない。 ある特別な状況で、そのために助けとなるのが |
|
ガロア理論における対称性と、基本群と被覆空間の理論における対称性との 間には強い類似性が認められる -- 例えば、どちらも対称性と対象物とを 正確に関係づける 「基本定理」を満たす。この根拠としては、被覆空間が代数方程式系で与えられる という事実があり、それらの方程式はガロア理論の研究対象である。 そのとき方程式系の対称性は、被覆空間の対称性と対応する。 この類似性を用いることにより、代数的な問題のいくつかを幾何学的な手法に より解くことができる。代表的な例としては、 整数の代わりに複素数を係数として考えた場合 (つまり、複素数体上の有理関数の体の上で考えた場合)に、 任意の対称性をあらわす群が 適切な方程式に対するガロア理論として実現される、 という事実を証明することができる。 不思議なことに、伝統的な有理数体上のガロア理論の状況で、これに 対応する主張はまだ証明されていない。ガロアの逆問題といわれる未解決問題 である。 |
|
この二つの研究領域の間には第二の関連がある。 それは被覆空間に対する方程式系が、(√2のような)代数的数と関わっている ところに由来している。すなわち、代数的数がそれ自身代数方程式の解である ため、ガロア理論により研究される範疇にはいるのである。 このことから、数論と代数と幾何が交錯する「被覆空間の算術性」の研究 に導かれる。この研究分野には、幾何学的に表現された様々な被覆の方程式に どのようなタイプの代数的数が現れるか、といった未解決の深い問題群が いくつも残されている。整数論に対するさらなる関連は、より一般的な空間、 例えば与えられた素数の倍数だけ座標がずれている2点を同等とみなす標数 p の世界、 などを考えることによりさらなる広がりをみせる。 この方向では、与えられた空間の上にどのような種類の対称性が存在し得るか、 あるいは空間が基本群によってどの程度決定されるか、を理解する問題 に限っても、最近において多大な進展が起こって来ている。 |